Fluid at Rest

Volume, Density, and Relative density

Volume: the volume of a liquid in cubic centimeters (cm3) or milliliters can be measured using any of the following

• Measuring cylinder
• Measuring flask
• Pipette or burette

The following formulas can be use to obtained the volume of a regular solid;

Volume of a sphere = 4πr3 where r is radius.                            

Volume of a box = l x b x t

            (i.e. length x breadth x thickness)

Volume of a cylinder = πr2 L  (where r is radius and L is height of cylinder)

Volume of a cone = 1/3  (base area x height)

 Density: the density of a substance is its mass per unit volume.

Density = mass/volume         Or    p = m/v

Note: p (rho) is a Greek letter representing density. SI unit of density is kgm-3.

Relative density (Rd.): the relative density (Rd.) of a substance is defined as follows:

Rd. = density of the substance/density of water

       =          mass of substance/ Mass of equal volume of water

       =            Weight of a substance/Weight of equal volume of water

Note: Relative density has no units.

Experimental diagram that determines solid, liquid and gas.

source: www.google.com

Pressure in fluid

Pressure is defined as the force acting normally (perpendicular) per unit area of surface.

Application of Pascal’s principle

Pascal’s principle states that the pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel.

Application of hydraulic press 

The general principle of hydraulic press is that pressure is transmitted equally to all parts of a liquid at the same level.

Formulas

P = F/A       (In Pa or Nm-2) F= force, A=area

P (rho)= density

P = W/A  = h p g (measured in pascals)

W= weight

Diagram of an hydraulic press

Source: www.google.com

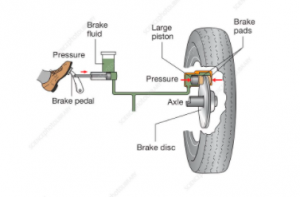
Diagram of a hydraulic device involving car brake system

source: www.google.com

   

Diagram of a manometer

Use: manometer is used to measure the pressure of gas in a container

source: www.google.com

Diagram of Magdeburg hemisphere

Uses: it is used to know the weight of air due to the fact that air has weight.

source: www.google.com

Diagram of a simple barometer

Uses: it is used to determine the altitude i.e. height of air.

Source: www.google.com

Diagram of a siphon

Uses: it is used for transferring liquid from a vessel such as a petrol tank which can not conveniently be emptied directly.

Source: www.google.com

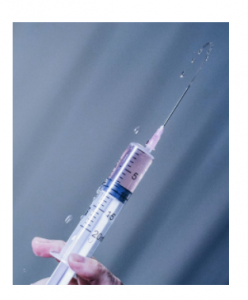
Diagram of a syringe

Uses: in syringe a piston is used to draw liquid into the cylinder. It can also be push out in the opposite direction for example in the hypodermic syringe used in medicine.

Source: www.google.com

Diagram of a pump

Uses: the common pump or lift pump is used for raising water from Wells 

Source: www.google.com

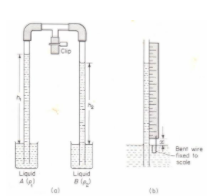
Note: The relative density of liquids using Hare’s apparatus

Diagram of Hare’s apparatus

Uses: it is used to know the relative density between a liquid of known density e.g. water and a liquid of whose density is required like oil.

source: www.google.com

Equilibrium of a body in a liquid

The force acting on a body while in water is called upthrust. Upthrust is an upward force acting on body.

T= W – U

Where W is the weight.

Archimedes’ principle states that when an object is wholly or partially immersed in a fluid, it experiences a loss in weight or an upthrust which is equal to the weight of the fluid displaced by the object.

Law of floatation states that an object will float in a fluid when the upthrust exerted upon it by the fluid in which it floats is equal to the weight of the object.

Past questions

1. The diagram above illustrates a simple barometer. Which distance measures the atmospheric pressure?(wassce 2018)

1. PQ
2. QR
3. RS
4. QS

Answer: A

2. A body weighing 14N in air is partially immersed in water. If the mass of the water displaced in the process is 200g, calculate the upthrust on the body. [g=10ms-2] (wassce 2017)

1. 2.0N
2. 3.0N
3. 3.5N
4. 7.0N

Answer: A

3. A pilot records the atmospheric pressure outside his plane as 63cm of Hg while a ground observer records a reading of 75cm of Hg with his barometer. Assuming that the density of air is constant, calculate the height of the plane above the ground (take the relative densities of air and Mercury as 0.00136 and 13.6 respectively) (wassce 1998)

1. 120m
2. 138m
3. 274m
4. 1,200m
5. 12,000m

Answer: E

4. The apparent weight of a body wholly immersed in water is 32N and its weight in air is 96N. Calculate the volume of the body.[Density of water = 1000kgm-3 g = 10ms-2]. (Wassce 2000)

1. 8.9 x 10-3m3
2. 6.4 x 103m3
3. 3.2 x 10-3m3
4. 3.0 x 103m3

Answer: B

5. The height at which the atmosphere ceases to exist is about 80km.

If the atmospheric pressure on the ground level is 760mmhg, the pressure at a height of 20km above the ground level is (jamb 2016)

1. 480mmhg
2. 570mmhg
3. 190mmhg
4. 380mmhg

Answer: A

6. Mercury is suitable as a barometric fluid because it (jamb 2016)

1. Expands uniformly
2. Is several times denser than water
3. Is opaque
4. Is a good conductor of heat

Answer: B

7. What volume of alcohol with a Density of 8.4 x 102kgm-3 will have the same mass as 4.2m3 of petrol whose density is 7.2 x 102kgm-3? (Jamb 1984)

1. 1.4m3
2. 3.6m3
3. 4.9m3
4. 5.0m3
5. 5.8m3

Answer: B

8. A heavy object is suspended from a string and lowered into water so that it is completely submerged. The object appears lighter because (jamb 1986)

1. The density of water is less than that of the object
2. The pressure is low just below the water surface 
3. It experiences an upthrust
4. The tension in the string neutralizes part of the weight

Answer: C